【最优传输】Optimal Transport最优传输笔记
1. 什么是最优传输
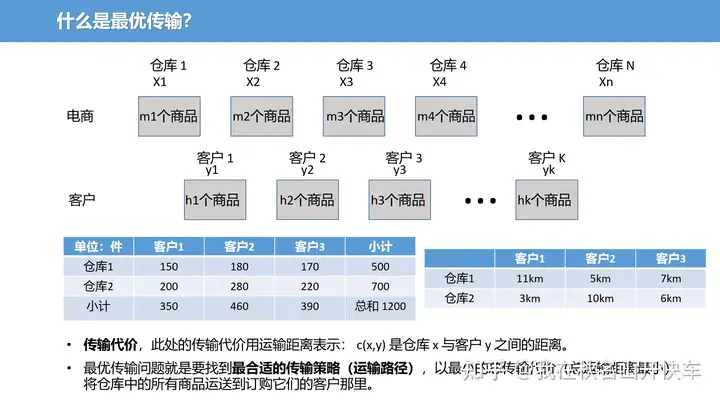

2. 基本概念
3.1 离散测度 (Discrete measures)
首先,说一下概率向量(或者称为直方图,英文:Histograms, probability vector)的定义:
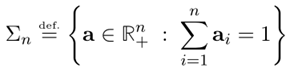
上述公式的含义:一个长度为n的数组,每个元素的值在[0, 1]之间,并且该数组的和为1,即表示的是一个概率分布向量。
比如[0.1,0.2,0.3,0.4]就是一个概率向量。
离散测度:所谓测度就是一个函数,把一个集合中的一些子集(符合上述概率分布向量)对应给一个数[4]。具体公式定义如下:
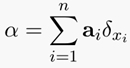
上述公式含义:以$a_i$为概率和对应位置$x_i$的狄拉克δ函数值乘积的累加和。下图很好地阐述了一组不同元素点的概率向量分布:

上图中红色点是均匀的概率分布,蓝色点是任意的概率分布。点状分布对应是一维数据的概率向量分布,而点云状分布对应的是二维数据的概率向量分布。
3.2 蒙日(Monge)问题
蒙日(Monge)问题的定义:找出从一个 measure(测度)到另一个measure的映射,使得所有$c ( x_i , y_j )$的和最小,其中$c$表示映射路线的运输代价,需要根据具体应用定义。蒙日问题具体的定义公式如下:
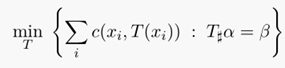
对于上述公式的解释可以采用离散测度来解释,对于两个离散测度:
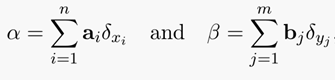
找到一个n维映射到m维的一个映射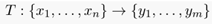 ,使得
,使得
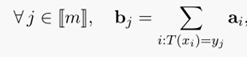
上述映射的示意图如下:
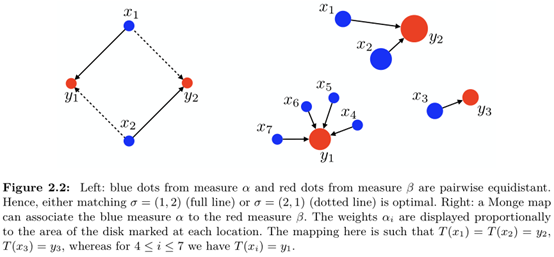
对于上述的映射公式,结合蒙日问题的定义公式,可以归纳如下:
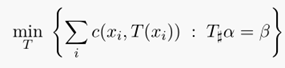
上述公式的含义:通过这个映射$T(x_i)$的转移,使得转移到$b_j$的所有$a_i$的值的和刚好等于$b_j$(其中要求,所有$a_i$必须转走,而所有$b_j$必须收到预期的货物),即我需要多少就给运输转移多少,不能多也不能少。其中$c()$表示运输代价,$T(x_i)$表示映射的运输方案。
3.3 Kantorovich Relaxation (松弛的蒙日问题)
蒙日问题是最优运输的起初最重要的思想,然而其有一个很大的缺点: 从a的所有货物运输到b时,只能采用原始的货物大小进行运算,即不能对原始的货物进行拆开发送到不同目的地。而Kantorovich Relaxation则对蒙日问题进行了松弛处理,即原始的货物可以分开发送到不同目的地,也可以把蒙日问题理解为Kantorovich Relaxation的一个映射运输特例。具体区别可以参考下图[2]。
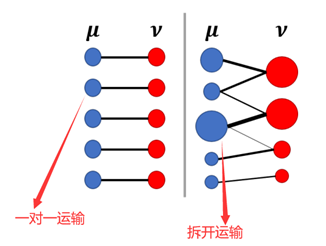
符合Kantorovich Relaxation的映射运输定义公式如下:
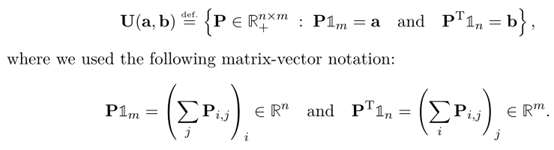
区别于蒙日问题要求映射运输的所有$a_i$一对一转走到$b_j$。Kantorovich Relaxation只要求,所有每个$a_i$中获取能够完全转走,可以是只转给一个$b_j$,也可以是多个$b_j$,但是要确保每个$b_j$只需要收取预期要求的货物即可。简单地描述:行求和对应向量a, 列向量求和对应向量 b.具体的传输示例如下:
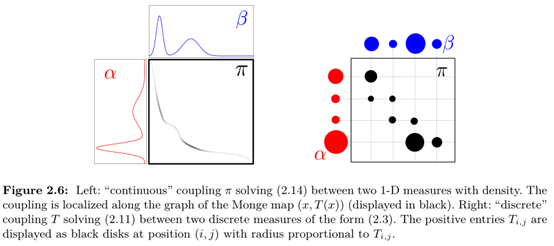
最后,Kantorovich Relaxation的最优运输求解公式定义如下:
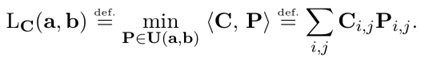
其中P表示符合所有行求和为向量a,所有列求和为向量b的一个映射。Pi,j表示从第i行映射到第j行的元素值,Ci,j表示完成Pi,j元素映射(或者说是运输)的运输代价。
3.5 最优运输问题求解

3.5.1 熵(Entropic)正则化
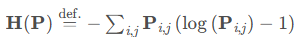
H(P)即为正则化的代价函数,是整个概念的核心。
那么加上正则化的最优传输问题则变为
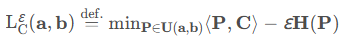
这里的$ε$是个正则化系数,它的大小决定正则化作用的强度,道理和神经网络里的正则化系数是完全一样的。
那么我们来分析正则化的作用。
$\sum{i, j} \mathbf{P}{i, j}=1$ 所以 $\log \left(\mathbf{P}_{i, j}\right)<0$ 绝对成立
同样一个单位的质量转移,如果是分布在少数的$\mathbf{P}{i,j}$上,每个$\mathbf{P}{i,j}$取值较大的情况代价会大于将质量分布在多个$ \mathbf{P}{i,j}$上,每个$\mathbf{P}{i,j}$取值很小的情况。
换句话说,正则化鼓励利用多数小流量路径的传输,而惩罚稀疏的,利用少数大流量路径的传输,由此达到减少计算复杂度的目的。
可以看到,在$ε$取值较小时,传输集中使用少数路径,然而当$ε$取值变大,正则化传输的最优解变得更加“扁平”,使用更多的路径进行传输。
3.5.2 Sinkhorn算法 (NIPS, 2013)
熵正则化仍然是一个概念,需要一个有效的算法,才能够释放它的潜力。
得到Sinkhorn算法的第一步在于换一种方式表达正则化后的问题
正则化后的Kantorovich问题的解可以写为以下形式:
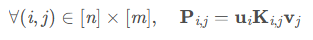
其中:
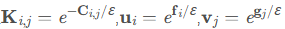
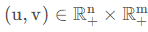
因为 $P=diag(u)Kdiag(v)$,而且根据之前的 “行求和对应向量a, 列向量求和对应向量 b”的条件,
所以有:
即

综上:P满足$P{i,j} = u_iK{i,j}v_j$,其中 u和v 要满足:$u\odot (Kv) = a$且$v\odot(K^Tu)=b$
。
这里$\odot$是元素对应的乘积。
这一对等式属于一类叫做matrix scaling的数学问题(matrix scaling problem),于是可以通过迭代方式求解,这两条等式作为之后迭代的收敛条件。
初始化:
也就是将v中每个元素都设为1
每一步先更新u满足左侧等式,再更新v满足右侧等式,最终迭代收敛,两侧等式同时满足,我们就得到了最优解
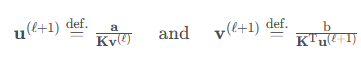
收敛后,再计算 P即可。
3. 参考链接
最优运输(Optimal Transfort):从理论到填补的应用 - 舞动的心 - 博客园 (cnblogs.com)
最优传输-Sinkhorn算法(第九篇)_Utterly Bonkers的博客-CSDN博客_sinkhorn
最优传输理论 Optimal Transport - 知乎 (zhihu.com)












