【算法】Topk问题

TopK问题

参考文章：

快速排序的几种常见实现及其性能对比_Sunshine_top的博客-CSDN博客

排序——快速排序（Quick sort）_努力的老周的博客-CSDN博客

面试官最喜爱的TopK问题算法详解 - 知乎 (zhihu.com)

拜托，面试别再问我TopK了！！！_架构师之路_的博客-CSDN博客

215. 数组中的第K个最大元素 - 力扣（Leetcode）

问题描述：

从arr[1, n]这n个数中，找出最大的k个数，这就是经典的TopK问题。

栗子：

从arr[1, 12]={5,3,7,1,8,2,9,4,7,2,6,6} 这n=12个数中，找出最大的k=5个。

1. 排序

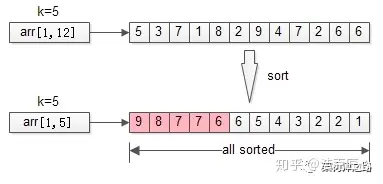
排序是最容易想到的方法，将n个数排序之后，取出最大的k个，即为所得。

伪代码：

sort(arr, 1, n);
return arr[1, k];

时间复杂度：O(n*lg(n))

分析：明明只需要TopK，却将全局都排序了，这也是这个方法复杂度非常高的原因。那能不能不全局排序，而只局部排序呢？这就引出了第二个优化方法。

2. 局部排序

不再全局排序，只对最大的k个排序。

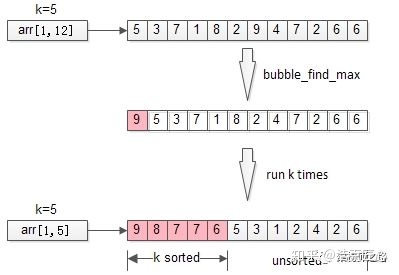
冒泡是一个很常见的排序方法，每冒一个泡，找出最大值，冒k个泡，就得到TopK。

伪代码：

for(i=1 to k){
	bubble_find_max(arr,i);
}
return arr[1, k];

时间复杂度：O(n*k)

分析：冒泡，将全局排序优化为了局部排序，非TopK的元素是不需要排序的，节省了计算资源。不少朋友会想到，需求是TopK，是不是这最大的k个元素也不需要排序呢？这就引出了第三个优化方法。

3. 堆

思路：只找到TopK，不排序TopK。

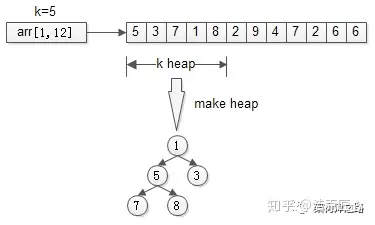
先用前k个元素生成一个小顶堆，这个小顶堆用于存储，当前最大的k个元素。

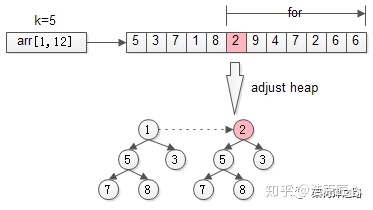
接着，从第k+1个元素开始扫描，和堆顶（堆中最小的元素）比较，如果被扫描的元素大于堆顶，则替换堆顶的元素，并调整堆，以保证堆内的k个元素，总是当前最大的k个元素。

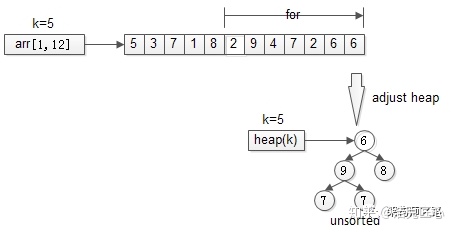
直到，扫描完所有n-k个元素，最终堆中的k个元素，就是猥琐求的TopK。

伪代码：

heap[k] = make_heap(arr[1, k]);

for(i=k+1 to n){
	adjust_heap(heep[k],arr[i]);
}
return heap[k];

时间复杂度：O(n*lg(k))

画外音：n个元素扫一遍，假设运气很差，每次都入堆调整，调整时间复杂度为堆的高度，即lg(k)，故整体时间复杂度是n*lg(k)。

分析：堆，将冒泡的TopK排序优化为了TopK不排序，节省了计算资源。堆，是求TopK的经典算法，那还有没有更快的方案呢？

4. 随机选择算法

随机选择算在是《算法导论》中一个经典的算法，其时间复杂度为O(n)，是一个线性复杂度的方法。

这个方法并不是所有同学都知道，为了将算法讲透，先聊一些前序知识，一个所有程序员都应该烂熟于胸的经典算法：快速排序。

4.1 快速排序回顾

算法思路
通过一趟排序将要排序的数据分割成独立的两部分，其中一部分的所有数据都比另外一部分的所有数据都要小，然后再按此方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，以此达到整个数据变成有序序列。

快速排序算法通过多次比较和交换来实现排序，其排序流程如下：

• 1、首先设定一个分界值，通过该分界值将数组分成左右两部分。

• 2、将大于或等于分界值的数据集中到数组右边，小于分界值的数据集中到数组的左边。此时，左边部分中各元素都小于或等于分界值，而右边部分中各元素都大于或等于分界值。

• 3、然后，左边和右边的数据可以独立排序。对于左侧的数组数据，又可以取一个分界值，将该部分数据分成左右两部分，同样在左边放置较小值，右边放置较大值。右侧的数组数据也可以做类似处理。

• 4、重复上述过程，可以看出，这是一个递归定义。通过递归将左侧部分排好序后，再递归排好右侧部分的顺序。当左、右两个部分各数据排序完成后，整个数组的排序也就完成了。

概括来说为 挖坑填数 + 分治法。

图解算法
快速排序主要有三个参数，left 为区间的开始地址，right 为区间的结束地址，Key 为当前的开始的值。

我们从待排序的记录序列中选取一个记录（通常第一个）作为基准元素（称为key）key=arr[left]，然后设置两个变量，left指向数列的最左部，right 指向数据的最右部。

第一步
key 首先与 arr[right] 进行比较，如果 arr[right]key则我们只需要将right—，right—之后，再拿arr[right]与key进行比较，直到arr[right]<key交换元素为止。

第二步
如果右边存在arr[right]key,则将arr[right]=arr[left]，如果arr[left]<key，则只需要将left++,然后再进行arr[left]与key的比较。

第三步
然后再移动right重复上述步骤。

第四步
最后得到 {23 58 13 10 57 62} 65 {106 78 95 85}，再对左子数列与右子数列进行同样的操作。最终得到一个有序的数列。
快排伪代码：

void quick_sort(int[]arr, int low, inthigh){
	if(low== high) return;
	int i = partition(arr, low, high);
	quick_sort(arr, low, i-1);
	quick_sort(arr, i+1, high);
}

java代码模板1：

class Solution {
    Random random = new Random();
    public int[] sortArray(int[] nums) {
        quickSort(nums,0, nums.length - 1);
        return nums;

    }
    //快排
    public int[] quickSort(int[] nums, int left, int right) {
        if(left < right) {
            int pos = partition(nums, left, right);
            quickSort(nums, left, pos - 1);
            quickSort(nums, pos + 1, right);
        }
        return nums;
    }

    public int partition(int[] nums, int left, int right) {
        int index = random.nextInt(right - left + 1) + left;
        int pivot = nums[index];
        nums[index] = nums[left];
        while (left < right) {
            while (left < right && nums[right] >= pivot) right--;
            nums[left] = nums[right];
            while (left < right && nums[left] <= pivot) left++;
            nums[right] = nums[left]; 
        }
        nums[left] = pivot;
        return left;
    }
}

java代码模板2：

class Solution {
    public int[] sortArray(int[] nums) {
        quickSort(nums,0,nums.length-1);
        return nums;
    }
    public void quickSort(int a[],int l,int r){
        if(l>=r)return;
        int x = a[l];
        int i = l - 1;
        int j = r + 1;
        while(i<j){
            do{i++;}while(a[i]<x);
            do{j--;}while(a[j]>x);
            if(i<j){
                int t = a[j];
                a[j] = a[i];
                a[i] = t; 
            }
        }
        quickSort(a,l,j);
        quickSort(a,j+1,r);
    }
}

4.2 随机选择算法与快排

快速排序核心算法思想是，分治法。

分治法（Divide&Conquer），把一个大的问题，转化为若干个子问题（Divide），每个子问题“都”解决，大的问题便随之解决（Conquer）。这里的关键词是“都”。从伪代码里可以看到，快速排序递归时，先通过partition把数组分隔为两个部分，两个部分“都”要再次递归。

分治法有一个特例，叫减治法。

减治法（Reduce&Conquer），把一个大的问题，转化为若干个子问题（Reduce），这些子问题中“只”解决一个，大的问题便随之解决（Conquer）。这里的关键词是“只”。

快速排序的核心是：

i = partition(arr, low, high);

这个partition是干嘛的呢？

顾名思义，partition会把整体分为两个部分。

更具体的，会用数组arr中的一个元素（默认是第一个元素t=arr[low]）为划分依据，将数据arr[low, high]划分成左右两个子数组：

• 左半部分，都比t大

• 右半部分，都比t小

• 中间位置i是划分元素

以上述TopK的数组为例，先用第一个元素t=arr[low]为划分依据，扫描一遍数组，把数组分成了两个半区：

• 左半区比t大

• 右半区比t小

• 中间是t

partition返回的是t最终的位置i。

很容易知道，partition的时间复杂度是O(n)。(把整个数组扫一遍，比t大的放左边，比t小的放右边，最后t放在中间N[i]。)

partition和TopK问题有什么关系呢？

TopK是希望求出arr[1,n]中最大的k个数，那如果找到了第k大的数，做一次partition，不就一次性找到最大的k个数了么？(即partition后左半区的k个数。)

问题变成了arr[1, n]中找到第k大的数。

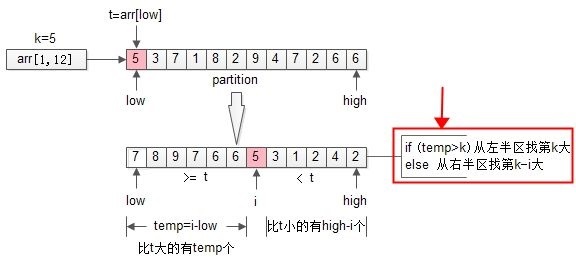
再回过头来看看第一次partition，划分之后：

i = partition(arr, 1, n);

如果i大于k，则说明arr[i]左边的元素都大于k，于是只递归arr[1, i-1]里第k大的元素即可；

如果i小于k，则说明说明第k大的元素在arr[i]的右边，于是只递归arr[i+1, n]里第k-i大的元素即可；

这就是随机选择算法randomized_select，RS，其伪代码如下：

int RS(arr, low, high, k){
	if(low== high) return arr[low];
	i= partition(arr, low, high);
	temp= i-low; //数组前半部分元素个数
	if(temp>=k){
        return RS(arr, low, i-1, k); //求前半部分第k大
    }else{
        return RS(arr, i+1, high, k-i); //求后半部分第k-i大
    }
}

时间复杂度:O(n);这里 N 是数组的长度,假设每次pivot都在中间O(以n为首项，1/2为等比数列q的等比数列的和) = O(n)

空间复杂度:O(n);

最后通过随机选择（randomized_select），找到arr[1, n]中第k大的数，再进行一次partition，就能得到TopK的结果。

例题：215. 数组中的第K个最大元素

给定整数数组 nums 和整数 k，请返回数组中第 **k** 个最大的元素。

请注意，你需要找的是数组排序后的第 k 个最大的元素，而不是第 k 个不同的元素。

你必须设计并实现时间复杂度为 O(n) 的算法解决此问题。

示例 1:

输入: [3,2,1,5,6,4], k = 2
输出: 5

示例 2:

输入: [3,2,3,1,2,4,5,5,6], k = 4
输出: 4

提示：

• 1 <= k <= nums.length <= 105
• -104 <= nums[i] <= 104

import java.util.Random;


class Solution {
    
    private final static Random random = new Random(System.currentTimeMillis());
    
    public int findKthLargest(int[] nums, int k) {
        int len = nums.length;
        int target = len - k;
        
        int left = 0;
        int right = len - 1;
        
        while (true) {
            int pivotIndex = partition(nums, left, right);
            if (pivotIndex == target) {
                return nums[pivotIndex]; 
            } else if (pivotIndex < target) {
                left = pivotIndex + 1; 
            } else {
                // pivotIndex > target
                right = pivotIndex - 1; 
            }
        }
    }
    
    public int partition(int nums[],int left,int right){
        int index = random.nextInt(right - left + 1) + left;
        int pivot = nums[index];
        nums[index] = nums[left];
        while (left < right) {
            while (left < right && nums[right] >= pivot) right--;
            nums[left] = nums[right];
            while (left < right && nums[left] <= pivot) left++;
            nums[right] = nums[left]; 
        }
        nums[left] = pivot;
        return left;
    }
    
}

• 时间复杂度：O(N)
• 空间复杂度：O(1)，没有使用递归，在逐渐缩小搜索区间的过程中只使用到常数个变量。