前言

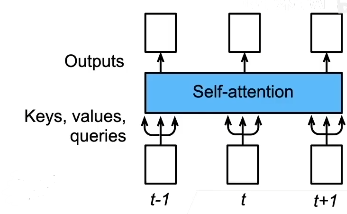
我们前面说过，注意力机制包含几个重要的参数，query，key，value，针对不同的问题，往往需要选择合适的变量来作为query，key,和value，当遇到query,key,value都是同一个东西，同一种参数的时候，这样的机制叫做自注意力机制。

1. 自注意力

假设我们有一个输入序列

$\mathbf{x}_{1}, \ldots, \mathbf{x}_{n}, \forall \mathbf{x}_{i} \in \mathbb{R}^{d}$

xi是第i个时间步的输入，d是输入值的特征维度，自注意力池化层将xi同时作为query,key,value，对序列抽取特征得到

$\mathbf{y}_{1}, \ldots, \mathbf{y}_{n}$

其中

$\mathbf{y}_{i}=f\left(\mathbf{x}_{i},\left(\mathbf{x}_{1}, \mathbf{x}_{1}\right), \ldots,\left(\mathbf{x}_{n}, \mathbf{x}_{n}\right)\right) \in \mathbb{R}^{d}$

xi作为query，key-value对包含了所有的xi对，对应序列中的每一个元素xi都会输出一个yi。

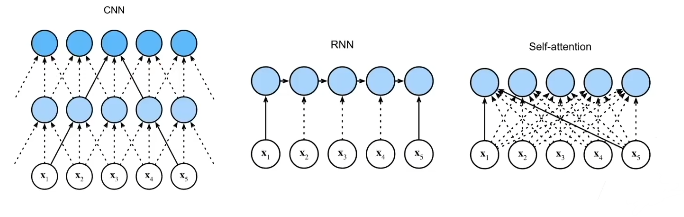
2. 与CNN,RNN对比

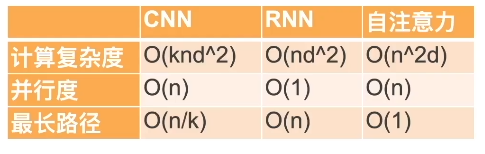
对于CNN，k就是指卷积核的大小，n是输入数据量，d是指数据维度，并行度就是说每个输出之间可以各自独立运算出结果，第一个输出的结果不取决于上一个输出，这样的话就很方便进行并行的计算，大家可以同时计算，这样的计算效率就比较高。

最长路径我理解的是输入信息在前向计算和反向传播过程中影响到另一个输入所需要走过的最长路径。

自注意力的计算复杂度比较高，尤其是输入序列较长的时候，根据之前计算yi的公式，我们需要把序列中的每个元素都进行计算，这带来了比较大的计算负担。但是最大路径很短，这在网路示意图中可以很明显的看到，当序列很长的时候可以很快获取到距离比较远的信息。且相较于RNN多级传递可以有较少的信息损失。

我们都知道RNN适合处理序列但处理长序列就会有长程依赖的问题，为了解决这个问题提出了LSTM，但LSTM正如它的名字长短时记忆网络，终究只是比较长的短时记忆网络，原有局限性有改善但是依旧存在，因此结合自注意力池化可以做得更好，付出的代价就是高昂的计算成本。

3. 位置编码

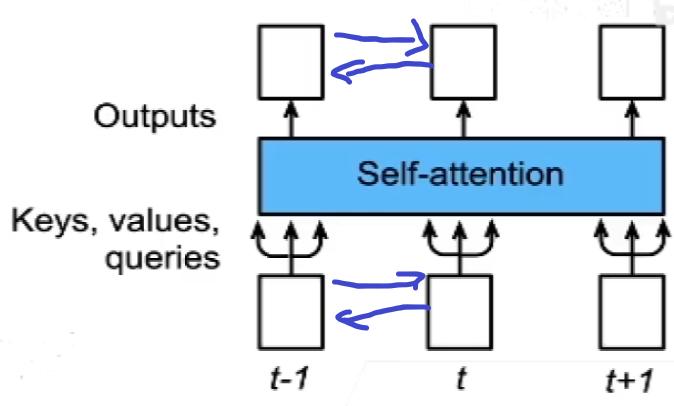
跟CNN和RNN不同，自注意力并没有记录位置信息。

意思就是当我输入序列顺序打乱，输出的顺序也会打乱，但是对应位置上的输出本身内容并不会发生改变，但是我们知道在处理序列的时候元素的顺序也是信息的一部分，比如在在翻译任务里面语序的不同往往对应不同的输出。

一个解决办法就是把位置信息添加到输入序列中，让输入数据本身就带有位置信息。

位置矩阵

假设长度为n的序列是$\mathbf{X} \in \mathbb{R}^{n \times d}$，那么使用一个位置编码矩阵$\mathbf{P} \in \mathbb{R}^{n \times d}$,将P加在X上，将X+P作为输入。其中P本身包含了许多关于X元素的位置信息，那么我们的目标就是找到一个合理的算法能够有效的提取X的位置信息并且存储在P里面。

P的计算公式如下：

$p{i, 2 j}=\sin \left(\frac{i}{10000^{2 j / d}}\right), \quad p{i, 2 j+1}=\cos \left(\frac{i}{10000^{2 j / d}}\right)$

i代表序列的第几个元素，即所谓的位置，j代表第几个特征维度。奇数列和偶数列不一样。

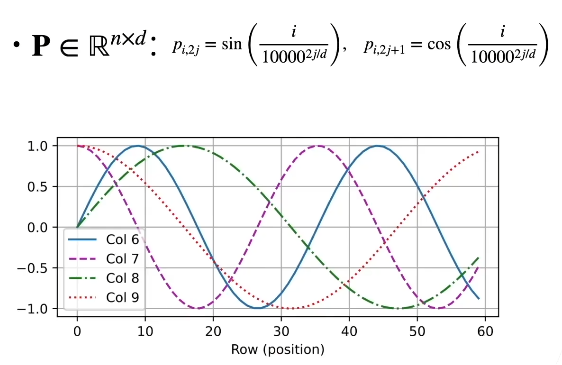
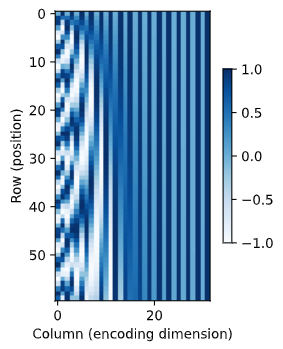
这是位置矩阵的图像。

途中的Row(position)对应的是位置矩阵的n，即第几个元素，不同的col列对应不同的特征维度。

模型需要有一定能力才能够学习到输入数据和位置信息之间的关系，这个位置矩阵存储的是相对位置信息。

我觉得可以借助信号处理的知识来理解这个位置矩阵，在信号与系统我们可以知道，对于任意一个时序信号我们都可以通过傅里叶变换将一个信号变换到频域，这个信号就会存在许多频域的分量。每一个频率分量在时域上进行叠加就得到一个完整的信号。

我们可以将输入序列X的每一维特征类比到频域的每一个频率分量即col6,col7都对应一个频率分量，然后不同的位置i或者时间点t即Row（position）就对应输入信号的不同的相位。不同的时间点i之间的差就可以类比相位差。

我们知道正弦信号具有周期性，所以其实相位差代表的就是相对位置关系，所以我们可以认为位置矩阵存储的是相对位置关系。

绝对位置信息

或者可以借助计算机使用的二进制编码来理解

0 in binary is 000
1 in binary is 001
2 in binary is 010
3 in binary is 011
4 in binary is 100
5 in binary is 101
6 in binary is 110
7 in binary is 111

我们也可以将$0~7$这个序列的每个元素都由长度为3的特征表示，低位的特征变化频率就比高位的变化要快。

相对位置信息

位置位于$i+\delta$处的位置编码可由线性投影位置$i$处的位置编码来表示

记$\omega_{j}=1 / 10000^{2 j / d}$，那么

$\left[\begin{array}{cc}\cos \left(\delta \omega{j}\right) & \sin \left(\delta \omega{j}\right) \ -\sin \left(\delta \omega{j}\right) & \cos \left(\delta \omega{j}\right)\end{array}\right]\left[\begin{array}{c}p{i, 2 j} \ p{i, 2 j+1}\end{array}\right]=\left[\begin{array}{c}p{i+\delta, 2 j} \ p{i+\delta, 2 j+1}\end{array}\right]$

这样就意味着输入序列的两个元素之间的相对位置关系固定的情况下，不管其中一个元素的绝对位置在哪，它们之间的相对位置关系都可以用同一个投影矩阵表示，毕竟这个投影矩阵和绝对位置$i$没有关系。如果要用一个参数$W$，表示相对位置关系采用这样的形式就可以不用顾及元素出现在序列的哪一个位置。

其实也可以用相位差来类比，正弦信号相乘会引起相位变化。