【机器学习】推荐系统 Factorization Machines 因子分解机

前言

因子分解机 (Factorization Machines) 是CTR预估的重要模型之一。要讲述因子分解机FM，就避不开逻辑回归LR（logistic Rgeression）和矩阵分解MF（Matrix Factorization）。

1.因子分解机的演变

传统的推荐模型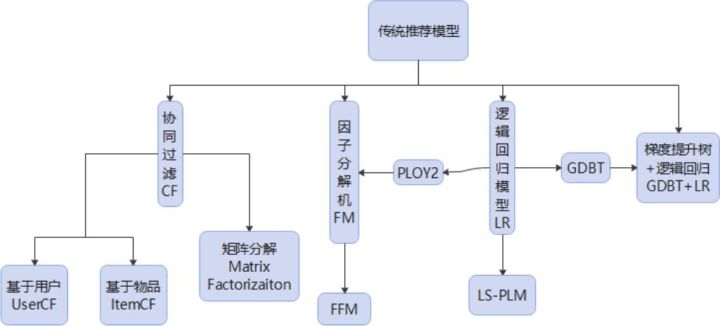

上图是传统的推荐系统模型的分类，逻辑回归LR模型在传统的推荐模型中占据着非常重要的位置。而因子分解机的出现，也来源于逻辑回归和矩阵分解的演化。

首先我们知道，逻辑回归的是对所有特征的一个线性加权组合, 然后再加入Sigmoid逻辑函数：

$\large \hat{y}(x)=w_{0}+w_{1} x_{1}+\ldots+w_{n} x_{n}=w_{0}+\sum_{i=1}^{n} w_{i} x_{i} \tag{1}$

对比与矩阵分解，虽然逻辑回归模型已经不单单考虑了用户的行为特征，也可以加入年龄，性别，物品的属性，时间，地点等等特征。但是逻辑回归表达能力仍然差的原因是仅仅用了每个单一的特征，而没有考虑到特征之间的关系。

那有没有模型可以加入特征之间的联系呢？

POLY2模型（Degree-2 Polynomial Margin）则在LR的基础上采用了一种暴力的特征组合模式，即将所有特征两两相交，因此原来的LR模型就变成了：

$\large \hat{y}(x)=w_{0}+\sum_{i=1}^{n} w_{i} x_{i}+\sum_{i=1}^{n-1} \sum_{j=i\llcorner 1}^{n} w_{i j} x_{i} x_{j} \tag{2}$

其中$\Large w_{i j}$是特征组合的$ (i, j)$权重。

也就是说，POLY2模型将所有的特征两两相交，暴力的组合了特征。这样以来，就增加了特征的维度，考虑到了特征之间的关系。但是同时，暴力的组合带来的是维度的增加。在机器学习中，我们普遍使用One-hot编码，这样的暴力组合，就使得复杂度从$\large n$上升到了 ,$\large n^2$ 特征维度也上升，同时数据极度稀疏，在训练过程中很难收敛。

那么有没有方法可以处理稀疏数据，同时保持特征之间的联系呢？

2.因子分解机

用户对电影打分的onehot编码

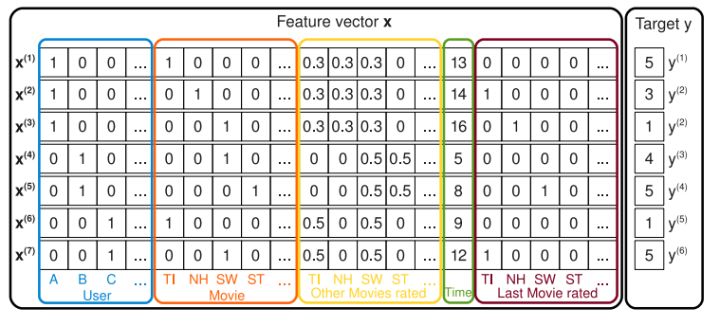
上图是电影背景下，用户对电影打分的onehot编码形式。每行代表一个样本，每列都代表一个特征。同时特征可以分为五个部分：用户ID，电影ID，用户对其他电影的打分（归一化），时间信息，以及对上一次电影的打分。

首先我们直观的看下，为什么POLY2模型在很多情况下是不适用的。

$\large \hat{y}(x)=w_{0}+\sum_{i=1}^{n} w_{i} x_{i}+\sum_{i=1}^{n-1} \sum_{j=i+1}^{n} w_{i j} x_{i} x_{j} \tag{3}$

POLY2模型的表达式如上， $\Large w{0}$是常数项， $\Large w{i}$是一阶特征的系数， $\Large w{i}w{j}$是二阶特征的系数，也就是交叉特征的系数。而由于在数据中，不是每个特征组合都有相互作用，因此， $\Large x{i}\cdot x{j}$为0。

举个例子来说，如上图中，我们要估计用户A对电影ST星际迷航（Star Trek）的相互作用，来预测A都ST的打分。显然，上图中A列乘以ST列是等于0的。也就是说，交叉项 $\Large x{i}\cdot x{j}$ 为0了，那么对应的 $\Large w{i}w{j}$ 在梯度更新时，$\Large\frac{\partial \hat{y}(x)}{\partial w{i, j}}=x{i} x{j}=0$，因此也就会导致 $\Large w{i}w_{j}$ 的训练不充分且不准确，进而影响模型的效果。

因此，因子分解机的应运而生。

因子分解机的优势是为每个特征学习了一个隐权重向量（latent vector），在特征交叉的时候，用这两个特征隐向量内积作为交叉特征的权重。如何理解这个含义呢？

在这里我们就要提一嘴矩阵分解。矩阵分解其实是将一个稀疏矩阵R分解为两个矩阵内积的形式，通过内积回乘，就能够得到一个满秩的矩阵。如果是电影的评分矩阵，也就是可以对未知的电影评分进行预测。具体可以看这篇文章：

而因子分解机FM就是在POLY2模型的基础上，融合了矩阵分解的思想。即，对二阶交叉特征的系数以矩阵分解的方式调整，让系数不再是独立无关的，同时解决数据稀疏导致的无法训练参数的问题：

$\large\hat{y}(\mathbf{x}):=w_{0}+\sum_{i=1}^{n} w_{i} x_{i}+\sum_{i=1}^{n} \sum_{j=i+1}^{n}\left\langle\mathbf{v}_{i}, \mathbf{v}_{j}\right\rangle x_{i} x_{j} \tag{4}$

其中，$\large w_{0} \in \mathbb{R}, \quad \mathbf{w} \in \mathbb{R}^{n}, \quad \mathbf{V} \in \mathbb{R}^{n \times k}, V$是一个$\large n * k$的向量矩阵，$\large n$是特征$\large x$的个数，$\large k$是个待确定的参数。

$\large \left\langle\mathbf{v}{i}, \mathbf{v}{j}\right\rangle$ 表示点乘,即向量对应位置乘积的和

$\large \left\langle\mathbf{v}_{i}, \mathbf{v}_{j}\right\rangle:=\sum_{f=1}^{k} v_{i, f} \cdot v_{j, f} \tag{5}$

由矩阵分解可知，对任意一个正定矩阵$\large \mathbf{W}$，都可以找到一个矩阵$\large \mathbf{V}$，$\large \mathbf{}$且在矩阵$\large \mathbf{V}$维度$\large k$足够大的情况下使得$\large \mathbf{W}=\mathbf{V} \cdot \mathbf{V}^{t}$成立。因此，通过矩阵分解用两个向量 $\Large v{i}$ 和 $\Large v{j}$ 的内积近似原先矩阵$\large \mathbf{W}$。

其次，在拆解为 $\large\mathbf{v}{i}$ 和之 $\large\mathbf{v}{j}$ 后，参数更新时是对这两个向量分别更新的，那么在更新时，对于向量，我$\large\mathbf{v}{i}$们不需要寻找到一组 $\Large x{i}$和 $\Large x{j}$同时不为0，我们只需要在$\large x{i} \neq 0$的情况下，找到任意一个样本$\large x{k} \neq 0$即可通过 $\Large x{i}x{k}$ 来更新 $\Large v{i}$ 。

我们举个例子来理解下上面的定义：

在商品推荐的场景下，样本有两个特征，分别是类品和品牌。某个训练样本的特征组合是（足球，阿迪达斯）。在POLY2模型中，只有当“足球”和“阿迪达斯”同时出现在一个训练样本中时，模型才能够学到这个组合特征对应的权重。而在因子分解机FM中，“足球”的的隐向量也可以根据（足球，耐克）进行更新。“阿迪达斯”的隐向量也可以根据（篮球，阿迪达斯）更新，由此一来，就大幅度的降低了模型对稀疏性的要求。

更极端的情况，对于一个从未出现的组合（篮球，耐克），因为模型已经学习了“篮球”和“耐克”的隐向量，因此就具备了更新权重 $\Large w$ 的能力，使其泛化能力大大提高。

3.降低时间复杂度

公式（3）的时间复杂度为 $O\left(k n^{2}\right)$ , 我们可以对二阶交叉特征进行化简，使时间复杂度降低到 $O\left(k n\right)$ 。

$\large \sum_{i=1}^{n} \sum_{j=i+1}^{n}\left\langle\mathbf{v}_{i}, \mathbf{v}_{j}\right\rangle x_{i} x_{j} \tag{6}$

首先矩阵A中的上三角，红色方框部分代表公式（6），也就是因子分解机中二阶交叉项部分。由图可以看出，他是矩阵的全部元素减去对角线元素之和得到的, 即：

$\large \sum_{i=1}^{n} \sum_{j=i+1}^{n}\left\langle\mathbf{v}_{i}, \mathbf{v}_{j}\right\rangle x_{i} x_{j}=\frac{1}{2}\left(\sum_{i=1}^{n} \sum_{j=1}^{n}\left\langle\mathbf{v}_{i}, \mathbf{v}_{j}\right\rangle x_{i} x_{j}-\sum_{i=1}^{n}\left\langle\mathbf{v}_{i}, \mathbf{v}_{i}\right\rangle x_{i} x_{i}\right)$

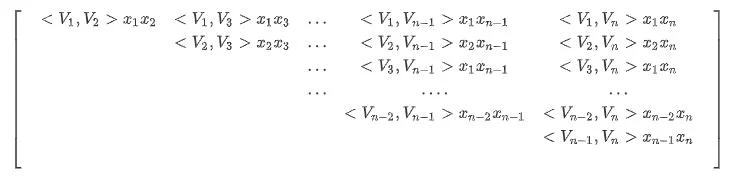
其中， $\large \sum{i=1}^{n} \sum{j=1}^{n}\left\langle\mathbf{v}{i}, \mathbf{v}{j}\right\rangle x{i} x{j}$ 是矩阵全部元素之和。 $\large \sum{i=1}^{n}\left\langle\mathbf{v}{i}, \mathbf{v}{i}\right\rangle x{i} x_{i}$代表对角线元素之和。

因为：

$\large \left\langle\mathbf{v}_{i}, \mathbf{v}_{i}\right\rangle=\sum_{f=1}^{k} v_{i, f}, v_{j, f}$

因此继续化简：

$\large =\frac{1}{2}\left(\sum_{i=1}^{n} \sum_{j=1}^{n} \sum_{f=1}^{k} v_{i, f} v_{j, f} x_{i} x_{j}-\sum_{i=1}^{n} \sum_{f=1}^{k} v_{i, f} v_{i, f} x_{i} x_{i}\right)$ $\large =\frac{1}{2} \sum_{f=1}^{k}\left(\left(\sum_{i=1}^{n} v_{i, f} x_{i}\right)\left(\sum_{j=1}^{n} v_{j, f} x_{j}\right)-\sum_{i=1}^{n} v_{i, f}^{2} x_{i}^{2}\right)$ $\large =\frac{1}{2} \sum_{f=1}^{k}\left(\left(\sum_{i=1}^{n} v_{i, f} x_{i}\right)^{2}-\sum_{i=1}^{n} v_{i, f}^{2} x_{i}^{2}\right) \tag{7}$

那么，因子分解机的二阶表达式就为：

$\large \hat{y}(x):=w_{0}+\sum_{i=1}^{n} w_{i} x_{i}+\frac{1}{2} \sum_{f=1}^{k}\left(\left(\sum_{i=1}^{n} v_{i, f} x_{i}\right)^{2}-\sum_{i=1}^{n} v_{i, f}^{2} x_{i}^{2}\right) \tag{8}$

其复杂度为 $O\left(k n\right)$ 。考虑到特征的稀疏性，尽管 $\large n$可能很大，但很多 $\Large x_{i}$ 都是零。因此其实际复杂度应该是 $O(k \bar{n})$ ,其中 $\large \bar{n}$表示样本不为零的特征维度数量的平均值。

4.因子分解机FM求解

我们对公式（8）求偏导，可以计算因子分解模型对参数的梯度：

当参数为 $\large w_{i}$ 时：

$\large \frac{\partial \hat{y}(x)}{\partial w_{0}}=1 \tag{9}$

当参数为 $\large w{i}$ 时，只跟它相关的 $\large x{i}$ 有关:

$\large \frac{\partial \hat{y}(x)}{\partial w_{i}}=x_i \tag{10}$

当参数为 $\large v_{i,f}$ 时:

$\large \begin{aligned} \frac{\partial \hat{y}(x)}{\partial v_{i, f}} &=\frac{\partial \frac{1}{2}\left(\left(\sum_{i=1}^{n} v_{i, f} x_{i}\right)^{2}-v_{i, f}^{2} x_{i}^{2}\right)}{\partial v_{i, f}} \\ &=\frac{1}{2}\left(2 x_{i} \sum_{i=1}^{n} v_{i, f} x_{i}-2 v_{i, f} x_{i}^{2}\right) \\ &=x_{i} \sum_{j=1}^{n} v_{j, f} x_{j}-v_{i, f} x_{i}^{2} \end{aligned} \tag{11}$

因此，因子分解机FM模型对参数的梯度为：

$\large \frac{\partial \hat{y}(x)}{\partial \theta}= \begin{cases}1, & \text { if } \theta \text { is } w_{0} \\ x_{i}, & \text { if } \theta \text { is } w_{i} \\ x_{i} \sum_{j=1}^{n} v_{j, f} x_{j}-v_{i, f} x_{i}^{2} & \text { if } \theta \text { is } v_{i, f}\end{cases} \tag{12}$

5.损失函数选取及算法流程

至此，我们就推导出了因子分解机的表达式以及参数的梯度。那么，损失函数在这里我们以以下两个为例, 并用梯度下降法求解：

回归问题：平方差损失函数

$\large Loss =\frac{1}{2} \sum_{i=1}^{n}\left(\hat{y}_{i}-y_{i}\right)^{2}$

求偏导得：

$\large \frac{\partial L}{\partial \hat{y}(x)}=(\hat{y}(x)-y)$

平方损失函数的梯度为：

$\large \frac{\partial L}{\partial \theta}=(\hat{y}(x)-y) * \frac{\partial \hat{y}(x)}{\partial \theta}$

分类问题：对数损失函数

$\large L o s s=\frac{1}{2} \sum_{i=1}^{n}-\ln \left(\sigma\left(\hat{y}_{i} y_{i}\right)\right)^{2}$

其中：

$\large \sigma(\hat{y} y)=\frac{1}{1+e^{-\hat{y} y}}$ $\large \frac{\partial(\sigma(\hat{y} y))}{\partial \hat{y}}=\sigma(\hat{y} y) *[1-\sigma(\hat{y} y)] * y$

对数函数下的梯度为：

$\large \frac{\partial L}{\partial \theta}=\frac{1}{\sigma(\hat{y} y)} * \sigma(\hat{y} y) *\left[1-\sigma(\hat{y} y] * y * \frac{\partial \hat{y}(x)}{\partial \theta}\right.$ $\large =[1-\sigma(\hat{y} y)] * y * \frac{\partial \hat{y}(x)}{\partial \theta}$