【目标检测】FCOS学习笔记
FCOS 学习笔记
FCOS: Fully Convolutional One-Stage Object Detection
1. 前言
目前大多数先进的目标检测模型,例如RetinaNet、SSD、YOLOv3、Faster R-CNN都依赖于预先定义的锚框。相比之下,本文提出的FCOS是anchor box free,而且也是proposal free,就是不依赖预先定义的锚框或者提议区域。通过去除预先定义的锚框,FCOS完全的避免了关于锚框的复杂运算,例如训练过程中计算重叠度,而且节省了训练过程中的内存占用。更重要的是,本文避免了和锚框有关且对最终检测结果非常敏感的所有超参数。由于后处理只采用非极大值抑制(NMS),所以本文提出的FCOS比以往基于锚框的一阶检测器具有更加简单的优点。
1.1 锚框的缺点
- 检测表现效果对于锚框的尺寸、长宽比、数目非常敏感,因此锚框相关的超参数需要仔细的调节。
- 锚框的尺寸和长宽比是固定的,因此,检测器在处理形变较大的候选对象时比较困难,尤其是对于小目标。预先定义的锚框还限制了检测器的泛化能力,因为,它们需要针对不同对象大小或长宽比进行设计。
- 为了提高召回率,需要在图像上放置密集的锚框。而这些锚框大多数属于负样本,这样造成了正负样本之间的不均衡。
- 大量的锚框增加了在计算交并比时计算量和内存占用。
2. 网络结构

其中classification对应的是分类损失,regression输出特征维度是4对应的是中心点相对于上下左右边界的距离,其中这个距离是在特征图尺度上表示的。
此外,中心点到四个边界的距离到原图上中心点到四个边界的实际距离存在如下的映射关系。l,r,t,b分别各自对应了上下左右的距离,s代表了原图到特征图的缩放尺度,还原到原图需要乘上相应的系数s。

3. 正负样本的匹配
3.1 正负样本分配
在传统基于Anchor-Based的检测算法中,通常是将设计的Anchor模板与Gt Box计算IOU,在一定范围内的才算作正样本,但是在FCOS算法舍弃了Anchor之后必须采用新的正负样本分配策略。
在特征图上的每个点,只要在某个GT Box内就可以算作正样本。2019年早期版本论文当中是采用的右边的策略,但是往往会产生很多低质量的正样本,因此在2020年版本的论文当中,选择使用GT Box内部的一个Sub Box即靠近中心的一个Box,落入Sub Box的点才算正样本,具体计算SubBox按如下公式计算得出,其中系数r需要手动设置。

4. 损失计算
4.1 中心度Centerness

通过多级预测之后发现FCOS和基于锚框的检测器之间仍然存在着一定的距离,主要原因是距离目标中心较远的位置产生很多低质量的预测边框。
在FCOS中提出了一种简单而有效的策略来抑制这些低质量的预测边界框,而且不引入任何超参数。具体来说,FCOS添加单层分支,与分类分支并行,以预测”Center-ness”位置。
Centerness计算公式:
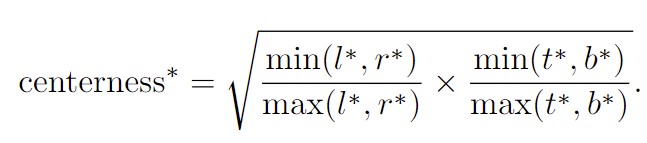
该策略之所以能够有效,主要是在训练的过程中我们会约束上述公式中的值,使得其接近于0,这就导致如下图中的蓝色框中的短边能够向黄边靠近,使得分布在目标位置边缘的低质量框能够尽可能的靠近中心。这样的话,在最终使用该网络的过程中,非极大值抑制(NMS)就可以滤除这些低质量的边界框,提高检测性能。

4.2 损失函数

5. Ambiguity问题
一个点可能同时被多个GT Box所包含,此时默认分配给面积最小的GT Box

使用FPN结构可以有效降低模糊Ambiguity的样本数。因为大部分发生重叠的样本往往尺度相差都比较大,通过FPN结构在不同尺度的特征图上进行预测的话,可以有效将不同尺度的GT Box分离,比如小面积的GT Box在高深层次的特征图上缩小没了,只留下了大尺度的GT Box.

在推理时,center-ness还有另一作用:类别权重. 在NMS时,其排序所用的置信度 sx,y 由center-ness ox,y 和类别概率 px,y 得到:
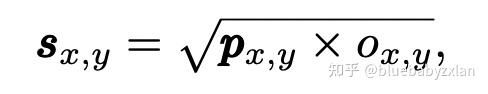
因此,距离GT中心越远的点,其center-ness ox,y越小,所得到的置信度sx,y就越小,因此NMS时会倾向于抑制该点. 此外,如下图所示,在对分类概率应用了center-ness后,具有低IoU但高置信度的检测框也有效的减少了

6. 不同尺度的目标与FPN的分配












