OTA阅读笔记

OTA: Optimal Transport Assignment for Object Detection

1. 什么是标签分配

为了训练目标检测器，需要为每个anchor 分配 cls 和 reg 目标，这个过程称为标签分配或者正采样。

cls指分类置信度，reg指检测框的偏移量。

通常基于Anchor的目标检测器会生成大量的预先定义好的Anchor,这些Anchor的数量是要远多于ground truth box的数量的。

以YOLOv3为例，每一个gt box最终都会有一个对应的Anchor，找到自己对应的gt box的Anchor算作正样本，没有找到的，比如Anchor坐标处在背景当中的算作负样本，另外有一部分会被直接忽略。

标签分配：三个特征图一共 8 × 8 × 3 + 16 × 16 × 3 + 32 × 32 × 3 = 4032 个anchor。

正例：任取一个ground truth，与4032个anchor全部计算IOU，IOU最大的anchor，即为正例。并且一个anchor，只能分配给一个ground truth。例如第一个ground truth已经匹配了一个正例anchor，那么下一个ground truth，就在余下的4031个anchor中，寻找IOU最大的anchor作为正例。ground truth的先后顺序可忽略。正例产生置信度loss、检测框loss、类别loss。标签为对应的ground truth标签（需要反向编码，使用真实的(x, y, w, h)计算出(tx, ty, tw, th) ）；类别标签对应类别为1，其余为0；置信度标签为1。

负例：正例除外（特殊情况：与ground truth计算后IOU最大的anchor，但是IOU小于阈值，仍为正例），与全部ground truth的IOU都小于阈值（0.5）的anchor，则为负例。负例只有置信度产生loss，置信度标签为0。
忽略样例：正例除外，与任意一个ground truth的IOU大于阈值（论文中使用0.5）的anchor，则为忽略样例。忽略样例不产生任何loss。
这样产生的问题是：一个GT只分配一个anchor来进行预测，存在正样本太少的问题，在后面的工作中例如FCOS已经证明了，增加高质量的正样本数量，有利于检测模型的学习。

2. 为什么提出OTA?

使用人工规则的分配方法，无法考虑尺寸、形状或边界遮挡的差异性。

当处理模糊标签时 (一个anchor可能对应多个目标)，对其分配任何一个标签都可能对网络学习产生负面影响。

OTA就是解决上述问题，以获得全局最优的分配策略。

3. OTA方法

3.1 最优传输问题(OT问题)回顾

松弛的蒙日问题

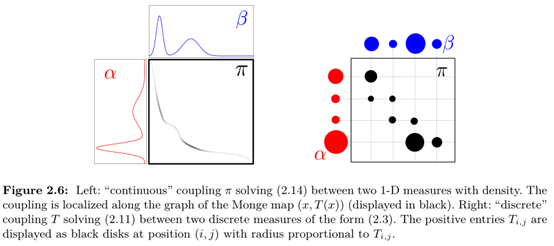
Kantorovich Relaxation的最优运输求解公式定义如下：

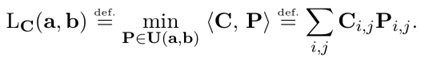
其中P表示符合所有行求和为向量a，所有列求和为向量b的一个映射。Pi,j表示从第i行映射到第j行的元素值，Ci,j表示完成Pi,j元素映射（或者说是运输）的运输代价。

3.2 Optimal Transport

假设第$i$个supplier拥有$s_i$个货物，第$j$个demander需要$d_j$个货物。

货物从supplier $i$运到demander $j$的成本为$c_{i,j}$。

目标是找到最佳运输方案$\pi^* = \pi_{i,j}|i = 1,2,…,m,j = 1,2,…,n$，可以让总的运输cost最低。

$\begin{gathered} \min _\pi \sum_{\mathrm{i}=1}^{\mathrm{m}} \sum_{\mathrm{j}=1}^{\mathrm{n}} \mathrm{c}_{\mathrm{ij}} \pi_{\mathrm{ij}} \\ \text { s.t. } \sum_{\mathrm{i}=1}^{\mathrm{m}} \pi_{\mathrm{ij}}=\mathrm{d}_{\mathrm{j}}, \sum_{\mathrm{j}=1}^{\mathrm{n}} \pi_{\mathrm{ij}}=\mathrm{s}_{\mathrm{i}}, \sum_{\mathrm{i}=1}^{\mathrm{m}} \mathrm{s}_{\mathrm{i}}=\sum_{\mathrm{j}=1}^{\mathrm{n}} \mathrm{d}_{\mathrm{j}} \\ \pi_{\mathrm{ij}} \geq 0, \mathrm{i}=1,2, \ldots, \mathrm{m}, \mathrm{j}=1,2, \ldots, \mathrm{n} \end{gathered}$

上述问题可以使用 Sinkhorn-Knopp算法来求解。

3.3 OTA思路

为了得到全局最优的分配策略，OTA方法提出将标签分配问题当作 Optimal Transport (OT) 问题。
具体来讲：

将每个gt当作可以提供一定数量labels的supplier，而每个anchor可以看作是需要唯一label的 demander，如果某个anchor从 gt 那儿获得足够的 label，那么这个 anchor就是此 gt 的一个正样本。

因为有很多anchor是负样本，所以还需引入另一个background供应商，专门为anchor提供 negative 标签，
问题目标是 supplier如何分配 label 给demander，可以让 cost 最低。其中 cost 的定义为：

对于每个anchor-gt pair，cost 为 pair-wise cls loss 和 pair-wise reg loss的加权和。
对于每个anchor-background pair，cost 为 pair-wise cls loss这一项。

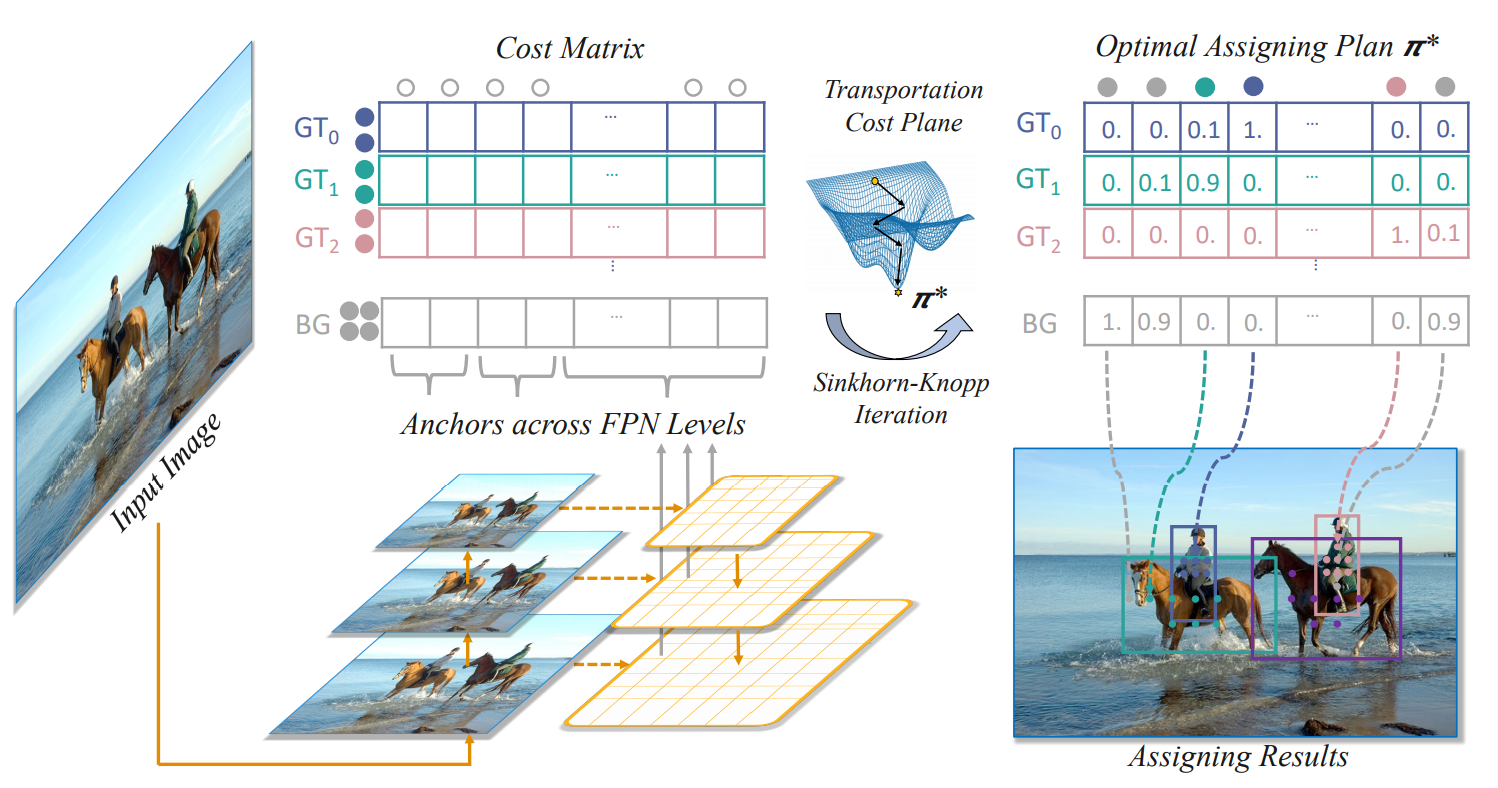
如上图所示，一张两个人骑马的图片，这张图片包含有四个gt box，其中彩色的点代表一些以该点为中心点的Anchor。我们要为这些彩色的点作标签分配，或者说正负样本匹配。

OTA算法的目的就是要通过对Cost Matrix矩阵使用Sinkhorn-Knopp最优传输迭代算法，找到一个使得”运输代价”Cost最小的一个传输矩阵$\pi$。传输矩阵$\pi$的形式，还是以上图为例，GT1给绿色点分配的label数量为0.9，给其他点分配的label数量则较少。

3.4 OT for Label Assignment

回到标签分配问题，对于一张图片，假设有 $m$ 个 gt 目标和 $n$ 个 anchors:

每个gt拥有$k$个positive lables,即$S_i = k;i = 1,2,…,m$
每个anchor需要一个lablel，即$d_j = 1;j = 1,2,…,n$

将一个positive label 从 $gti$运到anchor$a_j$的成本为$c^{fg}{ij}$,其可以表示为:

$c^{fg}_{ij} = L_{cls}(P^{cls}_j(\theta),G^{cls}_i) + \alpha L^{reg}(P^{box}_j(\theta),G^{box}_i)$

式中：

$P^{cls}_j$和$P_j^{cls}$分别表示对anchor $a_j$预测的cls score和bbox;

$G_i^{cls}$和$G_i^{box}$分别表示对$gt_i$的cls和bbox;

$L{cls}和L{box}$分别表示cross entropy loss和IoU Loss;

$\alpha$是2个Loss的平衡系数

此外很多anchor是负样本，所以还有一个background supplier，将一个negative label 从background supplier 运到 anchor $a_j$的成本为$c_j^{bg}$，其可以表示为:

$c_j^{bg} = L_{cls}(P_j^{cls}(\theta),\phi)$

可以计算出negative lables的总数为：$ n-m\times k$所以$s_i$更新为：

$s_i=\left\{ \begin{aligned} k & & i\leq m \\ n - m\times k & & otherwise \end{aligned} \right.$

4. OTA实施细节

为了便于理解，我们假设：

一张图片上有 3个目标框，即 3个ground truth
项目有 2个检测类别，比如 cat/dog
网络输出1000个预测框，其中只有少部分是正样本，绝大多数是负样本
bboxes_preds_per_image 是候选检测框的信息，维度是[1000，4]。预测框的四个坐标。

obj_preds 是目标分数(object score)，维度是 [1000，1]。预测框是前景还是背景。

cls_preds 是类别分数，维度是 [1000，2]。预测框的2个检测类别的one-hot。

训练网络需要知道这 1000个预测框的标签，而如何分配标签呢？

先附一张原论文描述的整体流程图

使用OTA方法，可以分为4步，具体做法如下：

step1: 生成cost矩阵

OTA方法分配标签是基于cost的，因为有3个目标框和1000个预测框，所以需要生成 3 × 1000 3\times 10003×1000 的 cost matrix，对于目标检测任务，cost 组成为位置损失和类别损失，计算方法如下：

定位损失

计算 3个目标框，和 1000个候选框，得到每个目标框和 1000 个预测框之间的 iou（pair_wise_ious)。

再通过 -torch.log 计算得到定位损失，即 pair_wise_iou_loss，向量维度为[3, 1000]。3 是 3个真实框，每个都计算1000个值。

1 2	pair_wise_ious=bboxes_iou(gt_bboxes_per_image,bboxes_perds_per_image,False) pair_wise_ious_loss=-torch.log(pair_wise_ious+1e-8)

分类损失

通过第一行代码，将类别的条件概率（cls_preds：表示分类的概率）和目标的先验概率（obj_preds：是前景的概率）做乘积，得到目标的类别分数(两个乘积得到的)。再通过第二行代码，F.binary_cross_entroy 的处理，得到 3个目标框和1000个预测框的综合loss值，得到类别损失，即 pair_wise_cls_loss，向量维度为 [3，1000]。3也是 3个真实框。其实这里就是算一个2分类交叉熵，cls_preds 和真实框的 1 算下。每个真实框算1000次。

1
2
3

cls_preds=(cls_preds_.float().unsqueeze(0).repeat(num_gt,1,1).sigmoid_()*obj_preds_.unsqueeze(0).repeat(num_gt,1,1).sigmoid_())

pair_wise_cls_losss=F.binary_cross_entropy(cls_pres_.sqrt_(),gt_cls_per_image,reduction='none').sum(-1)

有了reg_loss和 cls_loss，将两个损失函数加权相加，就可以得到cost成本函数了。

cost 计算公式如下：

$C_{ij} = L_{ij}^{cls} + \lambda L_{ij}^{reg}$

加权系数$\lambda=3$，计算代码如下：

1
2
3

cost=pair_wise_cls_loss
	  +3.0*pair_wise_ious_loss
	  +100000.0*(~is_in_boxes_and_center)

step2: dynamic_k_estimation

每个 gt 提供多少正样本，可以理解为“这个 gt 需要多少个正样本才能让网络更好的训练收敛”。

直觉上，每个gt 的大小、尺度和遮挡条件不同，所以其提供的positive albel数量也应该是不同的，如何确定每个gt的正样本数 $k$值呢，论文提供了一个简单的方案，该方法称之为：Dynamic k Estimation，具体做法如下：

从前面的 pair_wise_ious 中，给每个真实框，挑选 10个iou 最大的预测框。因为前面假定有3个目标，因此这里topk_ious的维度为[3，10]。 其实这里就是对于每个真实框选出来的 1000 个 IOU 值中选出来十个。

topk_ious 计算代码如下：

1
2
3

ious_in_boxes_matrix = pair_wise_ious
n_candidate_k = min(10, ious_in_boxes_matrix.size(1))
topk_ious, _ = torch.topk(ious_in_boxes_matrix, n_candidate_k, dim=1)

下面通过topk_ious的信息，动态选择候选框。dynamic_k_matching 代码如下:

1	dynamic_ks = torch.clamp(topk_ious.sum(1).int(), min=1)

针对每个目标框，计算所有anchor的 iou 值之和，再经过torch.clamp函数，得到最终右面的dynamic_ks值，给目标框1和3各分配3个候选框，给目标框2分配4个候选框。

step3: Sinkhorn-Knopp Iteration 求解 cost 矩阵获得标签分配方案

有了cost矩阵,$c$,supplying vector $s \in R^{m+1}$,demanding vector $d \in R^n$,因此可以通过现有的最有传输迭代算法Sinkhorn-Knopp Iteration，对该OT问题进行求解,从而得到最优运输方案$\pi ^ \in R^{(m+1) \times n}$。在得到$\pi ^ $之后，将每个anchor分配给运送labels 量最大的supplier(真实框)，从而解码出相应的标签分配方案。

step3: 得到matching_matrix（SimOTA中采用的简化版本）

1
2
3

for gt_idx in range(num_gt):
    _, pos_idx = torch.topk(cost[gt_idx], k=dynamic_ks[gt_idx], largest=False)
    matching_matrix[gt_idx][pos_idx] = 1

针对每个目标框挑选相应的 cost值最低的一些候选框。比如右面的matching_matrix中，cost值最低的一些位置，数值为1，其余位置都为0。

因为目标框1和3，dynamic_ks值都为3，因此matching_matrix的第一行和第三行，有3个1。而目标框2，dynamic_ks值为4，因此matching_matrix的第二行，有4个1。

step4: 过滤不同gt box共用的anchor候选框

anchor_matching_gt = matching_matrix.sum(0)
if (anchor_matching_gt > 1).sum() > 0:
    _, cost_argmin = torch.min(cost[:, anchor_matching_gt > 1], dim=0)
    matching_matrix[:, anchor_matching_gt > 1] *= 0
    matching_matrix[cost_argmin, anchor_matching_gt > 1] = 1

matching_matrix种第5列有两个1，这说明第5列所对应的候选框，被目标检测框1和2都进行关联。

因此对这两个位置，还要使用cost值进行对比，选择较小的值，再进一步筛选。假设第5列两个位置的值分别为0.4和0.3。

经过第三行代码，可以找到最小的值是0.3，即cost_min为0.3，所对应的行数，cost_argmin为2。

经过第四行代码，将matching_matrix第5列都置0。

再利用第五行代码，将matching_matrix第2行，第5列的位置变为1。

最终我们可以得到3个目标框，最合适的一些候选框，即matching_matrix中，所有1所对应的位置

5. OTA和SimOTA的区别

从上面描述可知，OTA 和 SimOTA 都是在经过 step2：dynamic_k_estimation 后，OTA 使用的是 Sinkhorn-Knopp Iteration 求解 cost 矩阵来获得最优的标签分配结果。SimOTA 是采用定义的规则使用 torch.topk 根据 dynamic_k_estimation 得到的 k ，选择 k 个 cost 最小的值，作为分配给真实框的候选框。

因此，SimOTA 有两个 topk ：1. step2：dynamic_k_estimation 中的选择比如 10 个 topk_ious。 2. 根据动态获得的 k 选择 k 个候选框。

OTA 只有 step2：dynamic_k_estimation 中的选择比如 10 个 topk_ious。