如何科学地利用高光谱图像合成对应的RGB图像?

1. 前言

参考链接:

色匹配函数是什么？ - 知乎 (zhihu.com)

23. 颜色知识1-人类的视觉系统与颜色 - 知乎 (zhihu.com)

色彩空间基础 - 知乎 (zhihu.com)

色彩空间表示与转换 - 知乎 (zhihu.com)

CIE XYZ - freshair_cn - 博客园 (cnblogs.com)

CIE 1931 color space - Wikipedia

CIE 1931色彩空间 - 维基百科，自由的百科全书 (wikipedia.org)

RGB/XYZ Matrices (brucelindbloom.com)

调色名词浅析——Gamma（伽玛）校正 - 知乎 (zhihu.com)

前置条件：

  • 必须有高光谱图像
  • 必须有波段信息，(你需要知道高光谱图像每个通道对应的波长是多少)

对于波段信息，我的波段信息是从软件ENVI中获取的txt文件
本文以128波段的高光谱图像为例，txt文件详细内容在文末给出

先上流程图，随后再逐一解释：

2. 计算色匹配函数

色匹配函数其实就是如下三条曲线(使用python手动绘制):

CIE-XYZ色匹配函数曲线如下:

2.1 什么是色匹配函数

追根溯源的话，得从我们人类的视网膜说起。大部分人类的视网膜上有三种感知颜色的感光细胞，叫做视锥细胞，分别对不同波长的光线敏感，称为 L/M/S 型细胞。三种视锥细胞最敏感的波长分别是橙红色（长波，Long），绿色（中波，Medium），蓝色（短波，Short）。这三种视锥细胞的归一化感光曲线如下图所示

img

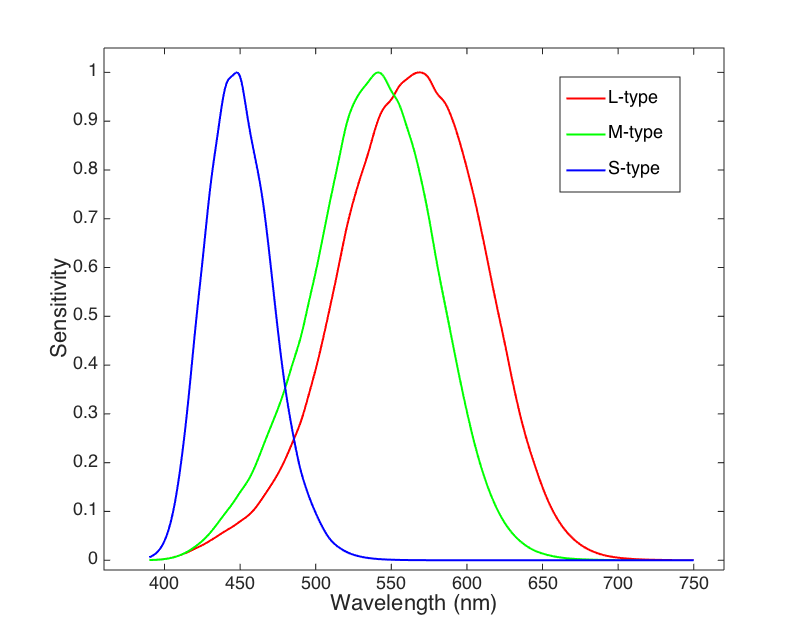
不仅如此，人类眼睛对不同颜色光线混合的反应还是 线性 的。根据 格拉斯曼定律（Grassmann’s Law）)，两束不同颜色的光$C_1$和 $C_2$，假设某个视锥细胞对他们的反应分别是 $r_1$ 和 $r_2$，现在将他们按照一个比例混合，得到第三种颜色 $C_3=\alpha C_1 + \beta C_2$，那么视锥细胞对这个混合颜色的反应也将是前两个反应的线性叠加 $r_3=\alpha r_1 + \beta r_2$。

格拉斯曼定律是一个实验规律，并没有物理或者生物学上的依据。然而这个规律大大简化了我们对人类彩色视觉系统的建模，并且给我们使用线性代数理论分析人类彩色视觉系统提供了一个前提和基础。

前面已经提到，人类视网膜上有三种感知色彩的视锥细胞，所以理论上我们用三种颜色的光就可以混合出自然界中任何一种颜色来。在 20 世纪 20 年代，David Wright 和 John Guild 各自独立地领导了一些实验，通过三种颜色的光源进行匹配，得到了人眼对于不同颜色光的匹配函数。此后，多名科学家多次进行了类似的实验，加深了我们对人类彩色视觉的认识。

实验过程大致是这样的，把一个屏幕用不透光的挡板分割成两个区域，左边照射某个被测试的颜色的光线，这里记为$C$（以下用大写字母表明颜色，用小写字母表明分量大小），右边同时用三种颜色的光同时照射，这里记为$R$，$G$，$B$。然后，调节右边三种颜色光源的强度，直到左右两边的颜色看上去一样为止。假设这个时候三种颜色的光源强度分别为$r$，$g$，$b$，那么根据光色叠加的线性性质，我们可以写出

也就是说，只要按照 (r,g,b) 的分量来混合 (R,G,B) 三种颜色的光，就可以得到 C 这个颜色的光。于是在这一系列实验里，科学家们把左边的颜色按着光谱顺序，挨个测试了一遍，得到了纯光谱色的混合叠加的数据，这就是 色匹配函数（Color Matching Function） ，并且在这个基准下定义的色彩空间，就是 CIE RGB 色彩空间。下图是 CIE RGB 的色匹配函数曲线，（图片数据来自CVRL main (ucl.ac.uk)）。浅色的细线代表实验中不同参与者个人的色匹配函数曲线，中间深色的粗线代表数据的平均值。

img

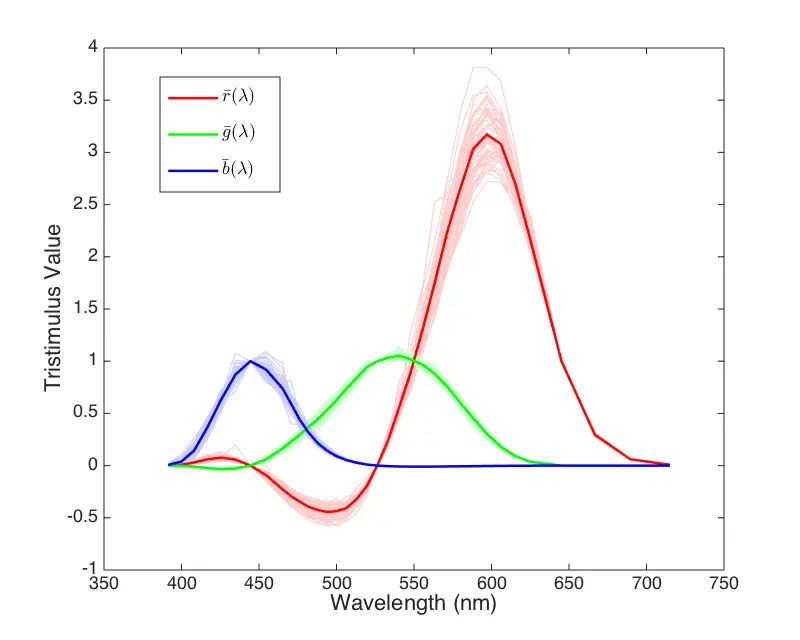
可以看到，曲线上出现了负数，这是怎么回事？回想一下前面描述的实验过程，左边是被测试的光色，右边是可调节的三色光的混合。如果碰到一种情况，右边三色光无论如何调节比例，都不能混合出左边的颜色，比如某种颜色的光强度已经减小为 0 了，然而看趋势还需要继续减小才能与左边的光色相匹配，怎么办？这时候需要往左边的光色中混入三色光中的一种或者几种，继续调节，直到两边的颜色匹配。在左边（被测试）的色光中添加，那就是相当于在右边的混合光中减去，这就导致了色匹配函数曲线上出现了负数。实际上，这相当于就是光线的「减法」了。

比如，对于 555nm 的黄色光，色匹配函数的值是 (1.30, 0.97, -0.01)，意味着将 1.30 份的红光与 0.97 份的绿光混合放在右边，左边放上 1 份的 555nm 的黄光，以及 0.01 份的蓝光，这样左右两边的光色看上去就一样了。

因为有部分出现了负数，在使用和计算上都有不方便，因此就对这个匹配函数进行了一下线性变换，变换到一个所有分量都是正的空间中。变换后的色彩空间就是 CIE XYZ 色彩空间。 （图片数据来自CVRL main (ucl.ac.uk)）

img

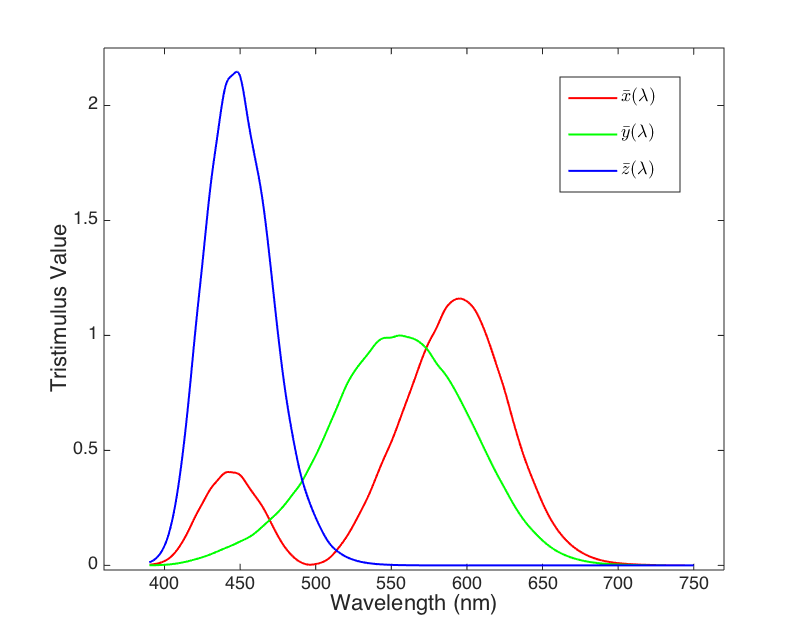
CIE RGB 色彩空间和 CIE XYZ 色彩空间是完全等价的，两者只是差了一个线性变换。由于允许「减法」的存在，因此 CIE RGB 空间是能够表示所有颜色的；同样的，CIE XYZ 空间也能。

在计算机问世之前，计算带有负值乘法的曲线是很麻烦的；XYZ就是为了把RGB空间转换成另一个没有负值的、方便计算的空间。很明显，XYZ的三色刺激值是想象出来的。

XYZ不用于描述颜色，而用于说明光波如何组合会产生什么样的颜色，因此XYZ是独立于设备的。

对于某些计算任务来说，查表可能变得不切实际。CIE XYZ颜色匹配函数可以通过高斯函数的和来近似。

设$g(x)$表示分段高斯函数，定义如下:

也就是说，$g(x)$类似于钟形曲线，其峰值在$x=μ$处，$σ1$的扩散/标准偏差在平均值的左侧，$σ2$的扩散在平均值右侧。使用以纳米为单位测量的波长$λ$，我们可以近似1931色匹配函数：

以上数据来自维基百科:CIE 1931 color space - Wikipedia

3. 根据光谱数据计算XYZ空间值

给定这些缩放了颜色匹配函数，带有频谱功率分布$I(\lambda)$的一个颜色的RGB 三色刺激值给出为：

实际上计算时多采用XYZ色彩空间，故对频谱分布函数积分时一般使用如下公式:

其中$\lambda$代表波长，$I(\lambda)$对应了该波段下的能量强度值(其实就是灰度值) 。

$\overline{x}(\lambda),\overline{y}(\lambda),\overline{z}(\lambda)$ 分别代表了刚才说的色匹配函数。

4. 将XYZ色彩空间变换到RGB色彩空间

由于 CIE RGB 和 CIE XYZ 两者其实是同一个线性空间的不同表达，因此两者的转换可以通过转换矩阵实现。

由于 CIE XYZ 空间是一个很方便的线性空间，与具体设备无关，因此常用来做各种颜色空间转换的中间媒介。设想某个颜色的光，经过色匹配函数的计算，得到了三个 XYZ 的值，如果直接将这三个值作为 RGB 颜色显示到屏幕上，显然是不对的。我们必须把 XYZ 的值转换到屏幕的 RGB 空间中的值。

由于不同的显示效果的需求，存在不同RGB色彩空间。不同的RGB色彩空间色域存在差异。

不同RGB色彩空间的转换矩阵在如下链接中可以找到:

RGB/XYZ Matrices (brucelindbloom.com)

因为白色参考点相关的内容确实还没有搞懂，但是对于本文要实现的目标不影响，所以挑选不同的转换矩阵尝试就好了，本文使用D50白色参考点，sRGB色域:

5. 伽马校正

在转换完之后，我们只是得到了一个线性的 RGB 值，要被显示器正确显示的话，还需要进行 gamma 校正。每个 RGB 空间对应的 gamma 校正公式不完全一致，大多数情况下都是 $C=C_{lin}^{1/\gamma}$，其中 $γ=2.2$，少数情况，比如 Apple RGB 采用的是 $γ=1.8 $的情况，再比如上面选择的 sRGB 空间，采用了一种分段的非线性函数进行校正：

在粗略的场景下，也可以直接使用 γ=2.2 的公式代替。

6. 代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
# coding=utf-8
import scipy.io as sio
import numpy as np
import cv2
import matplotlib.pyplot as plt
import os
import re


class GeneratorRGB:

    def __init__(self, wave_length):
        # 波长
        self.wavelengths = wave_length
        # self.transform_matrix = [[2.36461385, -0.89654057, -0.46807328],
        #                          [-0.51516621, 1.4264081, 0.0887581],
        #                          [0.0052037, -0.01440816, 1.00920446]]
		# 转换矩阵
        self.transform_matrix = [[3.1338561, -1.6168667, -0.4906146],
                                 [-0.9787684, 1.9161415, 0.0334540],
                                 [0.0719453, -0.2289914, 1.4052427]]
	# g(x;u,sigma1,sigma2)
    def piecewise_gaussian(self, x, u, sigma1, sigma2):
        return np.where(x < u, np.exp(-0.5 * (x - u) ** 2 / sigma1 ** 2), np.exp(-0.5 * (x - u) ** 2 / sigma2 ** 2))

    def x_gaussian(self, wavelength, adj=None):
        if not adj:
            adj = [{"u": 0, "sigma1": 0, "sigma2": 0},
                   {"u": 0, "sigma1": 0, "sigma2": 0},
                   {"u": 0, "sigma1": 0, "sigma2": 0}]
        result = 0.362 * self.piecewise_gaussian(wavelength,
                                                 442.0 + adj[0]["u"],
                                                 16.0 + adj[0]["sigma1"],
                                                 26.7 + adj[0]["sigma2"])
        result += -0.065 * self.piecewise_gaussian(wavelength,
                                                   501.1 + adj[1]["u"],
                                                   20.4 + adj[1]["sigma1"],
                                                   26.2 + adj[1]["sigma2"])
        result += 1.056 * self.piecewise_gaussian(wavelength,
                                                  599.8 + adj[2]["u"],
                                                  37.9 + adj[2]["sigma1"],
                                                  31.0 + adj[2]["sigma2"])
        return result

    def y_gaussian(self, wavelength, adj=None):
        if not adj:
            adj = [{"u": 0, "sigma1": 0, "sigma2": 0},
                   {"u": 0, "sigma1": 0, "sigma2": 0}]
        result = 0.286 * self.piecewise_gaussian(wavelength,
                                                 530.9 + adj[0]["u"],
                                                 16.3 + adj[0]["sigma1"],
                                                 31.1 + adj[0]["sigma2"])
        result += 0.821 * self.piecewise_gaussian(wavelength,
                                                  568.8 + adj[1]["u"],
                                                  46.9 + adj[1]["sigma1"],
                                                  40.5 + adj[1]["sigma2"])
        return result

    def z_gaussian(self, wavelength, adj: list = None):
        if not adj:
            adj = [{"u": 0, "sigma1": 0, "sigma2": 0},
                   {"u": 0, "sigma1": 0, "sigma2": 0}]
        result = 0.980 * self.piecewise_gaussian(wavelength,
                                                 437.0 + adj[0]["u"],
                                                 11.8 + adj[0]["sigma1"],
                                                 36.0 + adj[0]["sigma2"])
        result += 0.681 * self.piecewise_gaussian(wavelength,
                                                  459.0 + adj[1]["u"],
                                                  26.0 + adj[1]["sigma1"],
                                                  13.8 + adj[1]["sigma2"])
        return result

        # color matching function

    # 计算色匹配函数值
    def get_CIE_XYZ_weights(self, adj_x: list = None, adj_y: list = None, adj_z: list = None):
        cie_x = self.x_gaussian(self.wavelengths, adj=adj_x)
        cie_y = self.y_gaussian(self.wavelengths, adj=adj_y)
        cie_z = self.z_gaussian(self.wavelengths, adj=adj_z)
        return cie_x, cie_y, cie_z
	
    # 显示CIE-xyz色匹配函数曲线
    def show_weights_curve(self, adj_x: list = None, adj_y: list = None, adj_z: list = None):
        # adj_x = [{"u": 50, "sigma1": 0, "sigma2": 0},
        #          {"u": 50, "sigma1": 0, "sigma2": 0},
        #          {"u": 50, "sigma1": 0, "sigma2": 0}]
        #
        # adj_y = [{"u": -50, "sigma1": 0, "sigma2": 0},
        #          {"u": -50, "sigma1": 0, "sigma2": 0}]
        #
        # adj_z = [{"u": 0, "sigma1": 10, "sigma2": 10},
        #          {"u": 0, "sigma1": 10, "sigma2": 30}]
        # rgb_generator.show_weights_curve(adj_x=adj_x, adj_y=adj_y, adj_z=adj_z)
        cie_x, cie_y, cie_z = self.get_CIE_XYZ_weights(adj_x=adj_x, adj_y=adj_y, adj_z=adj_z)
        plt.figure("xyz_cmf")
        plt.xlabel("wave length/nm")
        plt.ylabel("value")
        plt.plot(self.wavelengths, cie_x, linewidth=1.5, color="r", label="x")
        plt.plot(self.wavelengths, cie_y, linewidth=1.5, color="g", label="y")
        plt.plot(self.wavelengths, cie_z, linewidth=1.5, color="b", label="z")
        plt.legend()
        plt.grid()
        plt.show()
	
    # 伽马校正
    def gamma_correction(self, rgb, gamma=1.5):
        rgb = np.power(rgb, 1 / gamma)
        return rgb
	# 将高光谱图像合成为RGB图像
    # 高光谱图像 宽width,高height,通道数channels
    # hyper_image.shape == (height,width,channels) 
    # adj_x,adj_y,adj_z,用来微调,u和sigma，改变xyz曲线的形状实现特殊效果
    def get_rgb(self, hyper_image, adj_x: list = None, adj_y: list = None, adj_z: list = None, BGR=True,
                gamma_correction=False):

        cie_x, cie_y, cie_z = self.get_CIE_XYZ_weights(adj_x=adj_x, adj_y=adj_y, adj_z=adj_z)
        X = np.sum(hyper_image * cie_x, axis=2)
        Y = np.sum(hyper_image * cie_y, axis=2)
        Z = np.sum(hyper_image * cie_z, axis=2)
        R = X * self.transform_matrix[0][0] + Y * self.transform_matrix[0][1] + Z * self.transform_matrix[0][2]
        G = X * self.transform_matrix[1][0] + Y * self.transform_matrix[1][1] + Z * self.transform_matrix[1][2]
        B = X * self.transform_matrix[2][0] + Y * self.transform_matrix[2][1] + Z * self.transform_matrix[2][2]
        if BGR:
            rgb_img = np.stack((B, G, R), axis=-1)
        else:
            rgb_img = np.stack((R, G, B), axis=-1)
        rgb_img = (rgb_img - np.min(rgb_img)) / (np.max(rgb_img) - np.min(rgb_img))
        if gamma_correction:
            rgb_img = self.gamma_correction(rgb_img)
        return rgb_img

# 根据txt波长信息生成对应的npy波长文件
def envitxt2npy(txt_path, npy_savepath):
    with open(txt_path) as f:
        lines = f.readlines()[3:]
        wavelengths = [float(re.findall(r"\d+\.?\d*", line)[0]) for line in lines]
    wavelengths = np.array(wavelengths)
    np.save(os.path.join(npy_savepath, "wavelengths_" + str(len(wavelengths)) + ".npy"), wavelengths)


if __name__ == "__main__":
    envitxt2npy("envi_plot.txt", ".")
    wavelengths = np.load("wavelengths_128.npy")
    # wavelengths_96 = wavelengths[31:223:2]
    rgb_generator = GeneratorRGB(wavelengths)

    rgb_generator.show_weights_curve()

7. 附录

波段信息txt文件，一共128个波段:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
ENVI ASCII Plot File [*** *** 24 11:45:14 1919]
Column 1: Wavelength
Column 2: n_D Class #1~~2##255,0,0
  371.700012   778.943339
  376.100006   770.241712
  380.500000   748.032550
  385.000000   711.031947
  389.399994   706.342978
  393.899994   694.409283
  398.299988   698.135021
  402.799988   710.817360
  407.299988   727.958409
  411.799988   737.475588
  416.299988   739.506932
  420.700012   754.845690
  425.200012   753.913201
  429.799988   766.892706
  434.299988   799.750452
  438.799988   835.210970
  443.299988   893.353225
  447.899994   924.624473
  452.399994   948.472574
  457.000000   921.470766
  461.500000   918.262809
  466.100006   917.420735
  470.700012   922.870404
  475.299988   952.725136
  479.899994   976.078360
  484.399994  1012.474985
  489.100006  1050.302592
  493.700012  1181.345992
  498.299988  1346.992164
  502.899994  1583.062086
  507.500000  1964.079566
  512.200012  2337.871609
  516.799988  2608.419530
  521.500000  2934.751055
  526.200012  3094.039783
  530.799988  3225.940928
  535.500000  3279.060880
  540.200012  3196.213382
  544.900024  3166.150090
  549.599976  3102.237492
  554.299988  3030.236890
  559.000000  2949.843882
  563.700012  2992.290536
  568.500000  2944.970464
  573.200012  2879.842676
  577.900024  2709.165160
  582.700012  2544.176612
  587.400024  2243.330319
  592.200012  2080.393008
  597.000000  1939.819168
  601.799988  1797.521398
  606.500000  1670.897529
  611.299988  1568.100663
  616.099976  1483.772152
  621.000000  1448.660639
  625.799988  1376.030741
  630.599976  1329.355636
  635.400024  1293.602170
  640.299988  1251.915009
  645.099976  1221.805907
  650.000000  1174.126582
  654.799988  1124.404461
  659.700012  1131.710066
  664.599976  1119.727547
  669.400024  1103.228451
  674.299988  1090.617842
  679.200012  1080.449066
  684.099976  1026.330922
  689.099976   993.049427
  694.000000  1033.698614
  698.900024  1022.889090
  703.799988  1008.230862
  708.799988   998.568415
  713.700012   962.066305
  718.700012   888.371308
  723.599976   878.981314
  728.599976   866.410488
  733.599976   888.247137
  738.599976   897.895118
  743.599976   917.882459
  748.599976   911.596745
  753.599976   914.708258
  758.599976   771.996986
  763.599976   730.689572
  768.599976   847.165160
  773.700012   855.122363
  778.700012   836.664858
  783.799988   827.171790
  788.799988   806.916817
  793.900024   790.221820
  798.900024   789.949367
  804.000000   809.836649
  809.099976   807.355033
  814.200012   784.625075
  819.299988   769.038577
  824.400024   786.312839
  829.500000   788.345389
  834.700012   806.656420
  839.799988   826.106088
  844.900024   827.244123
  850.099976   827.270645
  855.200012   816.968053
  860.400024   824.337553
  865.500000   814.603978
  870.700012   798.827004
  875.900024   796.328511
  881.099976   787.040386
  886.299988   772.019289
  891.500000   761.085594
  896.700012   742.569620
  901.900024   697.479204
  907.099976   697.937312
  912.400024   680.795660
  917.599976   674.689572
  922.900024   671.657625
  928.099976   671.411694
  933.400024   649.347197
  938.700012   619.044605
  943.900024   624.757083
  949.200012   619.104882
  954.500000   621.953586
  959.799988   610.510549
  965.099976   612.142857
  970.400024   613.606992
  975.700012   621.637734
  981.099976   613.901145
  986.400024   615.367691
  991.700012   616.359253